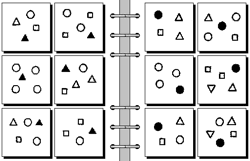
Bongard problems are an interesting way to challenge students to make discoveries using problem solving methods. An example (from the site linked at the beginning of this post) is shown below (hit ‘More’). All the Bongard problems have the same underlying premise: the group of six image/object collections on the left are united by some principle that is present in none of the six collections on the right. While it’s easy and fun to simply play this as a game, it’s another example of ‘discovery science’ based puzzle activities a la Petals Around the Rose or PatternMaster.
How are the six groups of objects on the left alike, and different from those on the right?
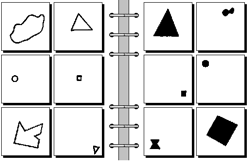
I’ve selected one that I think is pretty straightforward, and so feel guilt free in pointing out that all the objects on the left are un-filled, and those on the right solid (black). Since that’s one of the first hypotheses that likely came to mind, the potential depth of the activity isn’t really well revealed. But it’s worth pointing out that potential hypotheses include
–number of objects (false; one per frame in both left and right)
–complex shapes (false; both sides contain simple [triangle] and complex [lower left])
–‘pointy’ vs. ‘curved’ (false; mostly pointy but both have a circle)
–size (false; both have a large object top left and both middle rows have small objects)
—I could go on, and so can you
The Big Idea here is that for less trivial problems (and boy are there some! While part of the fun is that it’s impossible for me to tell if the ones I find difficult will be the ones you are flummoxed by, Number 28 is not solving itself for me right now). These trickier ones are an incredible playground for developing different problem solving strategies (some basic ideas from this blog here or here).
At first, you can just rattle through strategies that ‘pop into your head’; if you land on a winner, no harm/no foul. Then (hopefully!) we all become more thoughtful and analytical. For example, I employed a ‘simplifying strategy’ of trying to find one ‘very comparable’ panel from each side to see if I could find a point of difference to focus on. While current efforts are failing me, what I am doing is
1) Focusing on specific information in hopes of a hypothesis
2) Once the hypothesis pops up, predict what I will see in other data, both on the left set and on the right
3) My failures so far often lead to related hypotheses (for example, hypothesis X about triangles may be reborn as hypothesis X about circles, or hypothesis not-X about circles, or triangles…)
4) I then iterate through the process, over and over again… exactly as real, discovery-based science takes place.
And yet… in many cases where I have exposed this to students, they deem it to be ‘fun’. That’s really important. If we can clearly demonstrate that this is directly and identically the ‘Scientific Method’ at play and follow up by linking it to historical and ongoing examples, I think we have a teachable moment here. Or, as I tried with unknown success one semester, week after week of teachable moments. I simply projected a different one of these before class started; students could engage or not as they saw fit. But the real opportunity here is the follow-up metacognitive moment. What are you doing after your initial hypothesis fails? How are you generating ideas? What leads to success (for example, my so-far-failing “simplify and focus” is a sound general strategy even if I haven’t gotten anything for it yet!).
This sort of puzzle can also highlight the tremendous potential value of collaborative efforts. Who knows where ideas come from? What is continually out of reach for me may be the first thing you hit upon as soon as you inspect the problem. Alternatively, your wrong idea may trigger an avalanche in my head that includes the solution… or that re-triggers your thinking.
In any event, I think these types of problem, where we are not ‘solving for X’ or ‘applying the tool we have been lecturing about for a week to new environment X’ but rather “discover a new thing!” are an important aspect of real scientific research that too rarely finds its way in front of students. Bongard problems are ideal because their use of black-and-white abstract forms requires zero background or vocabulary and has everyone on equal footing. The challenge then becomes to extend into cases more likely to be recognized by students as ‘science’ and more directly engaging of the content we’re also charged with conveying.
Semi-related: the other thing I love is there are no ‘answers in the back of the book’, at least for this collection. If an answer works, it works, and is therefore correct. Period. You have twelve independent ‘pieces’ of data against which to test each hypothesis.